Блог

Процедура разложения изображения на пространственные частоты и соответственно обработка этого же изображения отдельно в каждой составляющей приобрела невероятную популярность. Вполне естественно появление отдельного специального фильтра Frequency Separation в АФ. В Adobe посчитали подобный шаг неинтересным, поэтому процедура разложения изображения на пространственные частоты осуществляется либо с использованием action либо вручную. По этому вопросу (выделения Frequency Separation в отдельный фильтр) мнения существуют разные. Мне думается, что лишним он (этот фильтр) не был бы. Тому примером чем-то даже родственный Frequency Separation фильтр  Unsharp Mask. Некоторые пользователи вручную вычитают из размытой (Unsharp-ной) копии оригинал и т. д. и т. д. чтоб получить Unsharp Mask и тому есть свои причины и логика, но большинство пользуются готовым фильтром. Он самодостаточен. Почему бы не сделать и такой же Frequency Separation.  Отвлёкся.

Итак. Чем хорош Frequency Separation в АФ.

Во-первых, он есть.

Во-вторых, он нагляден. Вы одновременно видите и высокочастотную и низкочастотную составляющие при выборе и изменении радиуса размытия.

В-третьих, при этом есть возможность выбора алгоритма размытия, что в некоторых случаях имеет немалое значение.

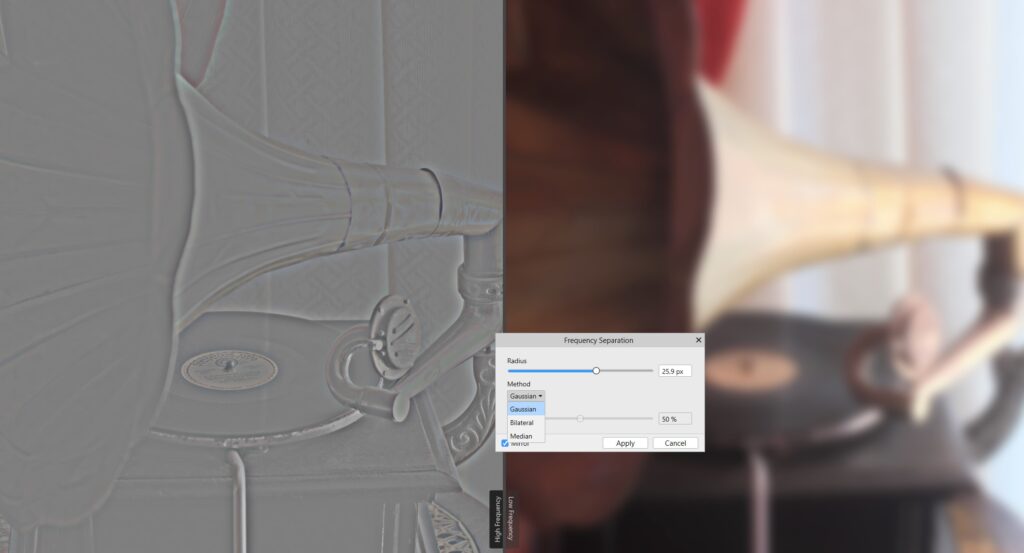
Из недостатков, ограничение двумя частотами (чего на самом деле хватает в большинстве случаев). Решается просто. Никто не запрещал Вам сделать всё вручную, чем мы далее и займёмся.Начнём всё таки с двух частот.

Конструкция выглядит так:

И макрос (это так в АФ обзывают экшены) в дополнение. FrqSp_2band

Должен честно признаться я не разобрался почему в АФ не нужно понижать вдвое контраст высокочастотной составляющей. Принял это как приятный (действительно приятный) сюрприз.

Разделение на составляющие с помощью Apply Image фотошоповским способом через Subtract наложение почему-то работает некорректно (тоже не разобрал почему). Зато использование математических формул (а такое возможно в АФ Apply Image) при формировании информации в канале даёт вполне адекватный результат.То есть мы применяем ту же формулу,что используется в Subtract-наложении, просто вводим её вручную.Плюс дополнительные манипуляции, описанные ниже

Напомню, нам нужно из размытой копии вычесть оригинал, уменьшить результат вдвое (чтобы вместиться в диапазон 0-1 (0-255) ) и сдвинуть на половину то есть  0,5 (128) (чтобы избежать отрицательных значений). Да уж…  Написал…  Но углубляться не буду. Дальше, я надеюсь, будет ясней.

Формула выглядит так: (SR-DR)/2+0.5 . Это для красного канала, для остальных соответственно.

Лучше на видео:

Ну и наконец, разложим на три частоты. Конструкция такая:

Плюс макрос. FrqSp_3band

Макросы в АФ оставляют желать лучшего, пожалуй даже много лучшего. Их нельзя остановить для ввода значений, он проигрывается от начала и до конца, но благо радиусы возможно поменять в уже готовой конструкции, только не забывайте о соответствии радиусов в HighPass и GaussianBlure.

Прежде чем закончить, упомяну ещё об одном фильтре, основанном на преобразовании в составляющие, а потом наоборот (всё же отойду от просторечия-это называется прямое дискретное преобразование и обратное дискретное преобразование Фурье). С лёгкой руки одного отличнейшего мастера ФШ «это» получило название «Фурье туда и обратно», просто и понятно (мне кажется). Это FFT(Fast Fourier Transform) Filter – фильтр на основе быстрого преобразования Фурье — в АФ он называется FFT Denoise.

Назначение у него специфическое и логично он находится в разделе фильтров Noise. Возможно в будущем мы уделим и ему внимание, а пока зловредно замечу, что в отличие от ФШ и такое  «добро» есть в АФ по умолчанию. Приятно. Интересный, кстати, фильтр.

Всё.

PS. Ну чтобы уж совсем по-перфекционистски… Сравним результат действия фильтра/экшена с оригиналом, посмотрим насколько отличаются результат разложения на частоты с первоисходным изображением. Коротче говоря, определим погрешность этих самых действий.Для этого схлопним два «частотных» слоя и наложим на оригинал в режиме Difference.Результат усилим кривыми. На кривых Х=0,012 соответствует значению 3 в ФШ (ФШ менее 4 поставить не даст,это минимальное значение в настройках кривых).

Итак, в 8-ми битном представлении разница впечатляет:

В 16-битном представлении разница также впечатляет, но наоборот.

Возможно на изображении не очень видно, но в АФ присутствуют детали (на уровне шумов, уровень чёрного от 0 до 4). Крайняя справа картинка дополнительно отображает правильное для 16-ти бит разложение (ApplyImage — Add инверсное наложение), но и это общую картину особенно не меняет.

Прокомментировать вышепоказанное не берусь, в реальной практике, мне кажется, подобные погрешности более, чем допустимы.

Ещё раз всё.